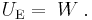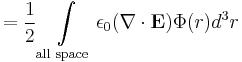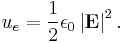Electric potential energy

Electric potential energy, or electrostatic potential energy, is a potential energy associated with the conservative Coulomb forces within a defined system of point charges. The term "electrostatic potential energy" is preferred here because it seems less likely to be misunderstood. The reference zero is usually taken to be a state in which the individual point charges are very well separated ("are at infinite separation") and are at rest. ^[1]^:§25-1 The electrostatic potential energy of the system (U_E), relative to this zero, is equal to the total work W that must be done by a hypothetical external agent in order to bring the charges slowly, one by one, from infinite separation to the desired system configuration:

$U_{\mathrm{E}} = \; W \;.$

In this process the external agent is deemed to provide or absorb any relevant work, and the point charge being slowly moved gains no kinetic energy.

Sometimes reference is made to the potential energy of a charge in an electrostatic field. This actually refers to the potential energy of the system containing the charge and the other charges that created the electrostatic field.^[1]^:§25-1

To calculate the work required to bring a point charge into the vicinity of other (stationary) point charges, it is sufficient to know only (a) the total field generated by the other charges and (b) the charge of the point charge being moved. The field due to the charge being moved and the values of the other charges are note required. Nonetheless, in many circumstances it is mathematically easier to add up all the pairwise potential energies (as below).

It is important to understand that electrostatics is a 18th-19th-century theory of hypothetical entities called "point charges". Electrostatics is categorically not a complete theory of the charged physical particles that make up the physical world, and are subject to the Heisenberg uncertainty principle and other laws of quantum mechanics.

1 Electrostatic potential energy stored in a configuration of discrete point charges
2 Energy stored in an electrostatic field distribution
3 Energy in electronic elements
4 References

Electrostatic potential energy stored in a configuration of discrete point charges

The mutual electrostatic potential energy of two charges is equal to the potential energy of a charge in the electrostatic potential generated by the other. That is to say, if charge 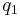$q_1$ generates an electrostatic potential $\Phi_1(\mathbf r)$ , which is a function of position $\mathbf r$ , then $U_E = q_2 \Phi_1(\mathbf r_2)$ . Also, a similar development gives $U_E = q_1 \Phi_2(\mathbf r_1)$ .

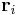This can be generalized to give an expression for a group of N charges, $q_i$ at positions $\mathbf r_i$ :

$U_E = \frac{1}{2}\sum_i^N q_i \Phi(\mathbf r_i)$

where, for each i value, 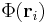$\Phi(\mathbf r_i)$ is the electrostatic potential due to all point charges except the one at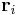 $\mathbf r_i$

Note: The factor of one half accounts for the 'double counting' of charge pairs. For example, consider the case of just two charges.

Alternatively, the factor of one half may be dropped if the sum is only performed once per charge pair. This is done in the examples below to cut down on the math.

One point charge

The electrostatic potential energy of a system containing only one point charge is zero, as there are no other sources of electrostatic potential against which an external agent must do work in moving the point charge from infinity to its final location. One should carefully consider the possibility of the point charge interacting with its own electrostatic potential. However, since such a potential at the location of the point charge itself is infinite, this "self-energy" is intentionally excluded from an evaluation of the total (finite) electrostatic potential energy of the system. Moreover, one may argue that since the electrostatic potential due to the point charge itself provides no work in moving the point charge around this interaction is unimportant for most purposes.

Two point charges

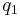Consider bringing a second point charge, $q_2$ , into its final position in the vicinity of the first point charge, $q_1$ . The electrostatic potential 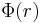$\Phi(r)$ due to 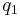$q_1$ is

$\Phi(r_1) = \; k_{\mathrm{e}} \frac{q_1}{r}$

where k_e is Coulomb's constant. In the International System of Quantities, which has been the preferred international system since the 1970s and forms the basis for the definition of SI units, the Coulomb constant is given by

$k_{\mathrm{e}} = \; \frac{1}{4 \pi \varepsilon_0}$ ,

where $\varepsilon_0$ is the electric constant. Hence we obtain,

$U_\mathrm{E} = \; \frac{1}{4\pi\varepsilon_0} \frac{q_1 q_2}{ r_{12}}$

where $r_{12}$ is the distance between the two point charges.

The electrostatic potential energy is negative if the charges have opposite sign and positive if the charges have the same sign. Negative mutual potential energy corresponds to attraction between two point charges; positive mutual potential energy to repulsion between two point charges.

Three or more point charges

For three or more point charges, the electrostatic potential energy of the system may be calculated by the total amount of work done by an external agent in bringing individual point charges into their final positions one after another. Thus,

$U_\mathrm{E} = \frac{1}{4 \pi \varepsilon_0} \left(\frac{q_1 q_2}{r_{12}} + \frac{q_1 q_3}{r_{13}} + \frac{q_2 q_3}{r_{23}} + \cdots + \frac{q_i q_j}{r_{ij}} \right)$

where

q₁, q₂, ..., are the point charges

r_ij is the distance between the ith and jth point charges.

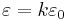Here, $\varepsilon_0$ is the permittivity of free space. When the charge is in a medium the relative permittivity, $\varepsilon = k\varepsilon_0$ , into account where k is the dielectric constant

Energy stored in an electrostatic field distribution

One may take the equation for the electrostatic potential energy of a continuous charge distribution and put it in terms of the electrostatic field.

Since Gauss' law for electrostatic field in differential form states

$\mathbf{\nabla}\cdot\mathbf{E} = \frac{\rho}{\epsilon_0}$

where

$\mathbf{E} \$ is the electric field vector
$\rho \$ is the total charge density including dipole charges bound in a material.

then,

$U = \frac{1}{2}\int \limits_{\text{all space}} \rho(r) \Phi(r)d^3r$

$= \frac{1}{2}\int \limits_{\text{all space}} \epsilon_0(\mathbf{\nabla}\cdot{\mathbf{E}})\Phi(r)d^3r$

so, now using the following divergence vector identity

$\nabla\cdot(\vec{A}{B}) = (\nabla\cdot\vec{A}){B} + \vec{A}\cdot(\nabla{B}) \Rightarrow (\nabla\cdot\vec{A}){B} = \nabla\cdot(\vec{A}{B}) - \vec{A}\cdot(\nabla{B})$

we have

$U = \frac{\epsilon_0}{2}\int \limits_{\text{all space}} \mathbf{\nabla}\cdot(\mathbf{E}\Phi) d^3r - \frac{\epsilon_0}{2}\int \limits_{\text{all space}} (\mathbf{\nabla}\Phi)\cdot\mathbf{E} d^3r$

using the divergence theorem and taking the area to be at infinity where $\Phi(\infty) = 0$

$U = \frac{\epsilon_0}{2}\int \Phi\mathbf{E}\cdot dA - \frac{\epsilon_0}{2}\int \limits_{\text{all space}} (-\mathbf{E})\cdot\mathbf{E} d^3r$

$= \int \limits_{\text{all space}} \frac{1}{2}\epsilon_0\left|{\mathbf{E}}\right|^2 d^3r.$

So, the energy density, or energy per unit volume of the electrostatic field is:

$u_e = \frac{1}{2} \epsilon_0 \left|{\mathbf{E}}\right|^2.$

Energy in electronic elements

Some elements in a circuit can convert energy from one form to another. For example, a resistor converts electrical energy to heat, and a capacitor stores it in its electric field.

The total electrostatic potential energy stored in a capacitor is given by

$U_{\textrm{E}} = \frac{1}{2} CV^2$

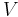where $C$ is the capacitance and $V$ is the total electrostatic potential.

References

↑ ^1.0 ^1.1 Halliday, David; Resnick, Robert; Walker, Jearl (1997). "Electric Potential" (in English). Fundamentals of Physics (5th ed.). John Wiley & Sons. ISBN 0-471-10559-7.